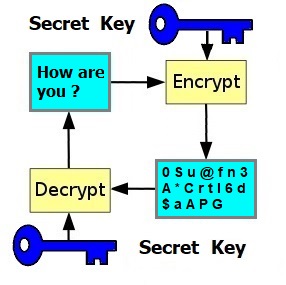
A way to encrypt some data using a secret key.
The same secret key will also decrypt the data.
In the diagram, encrypting the message: How are you ? with the secret key
produces the encrypted message: 0Su@fn3A*Crtl6d$aAPG.
The same secret key is used to decrypt: 0Su@fn3A*Crtl6d$aAPG
back to How are you ?
One disadvantage of this method is that when you are sending data encrypted this way to someone, they also require the secret key to decrypt it.
So how do you send it to them without a malicious individual intercepting it? We recommend using a different transmission method than what you used to send the data. e.g. if you sent the data by email, send the secret key as a text message or call the receiver.
The Data Krypter™ encrypts data using the PERNG algorithm.
PERNG Symmetric Encryption Algorithm:
A property of a good encryption method is that making a small change to the data to be encrypted, results in a big change to the encrypted data. How would this property apply to the case of encrypting a pair of characters? If one of the characters is changed (a small change) we want both of the characters (a big change) in the encrypted version to change.
e.g. encrypting the pair: PX might result in the encrypted version: AN. Changing either character in the original should result in both of the encrypted ones changing.
Here are some examples:
PX is encrypted as AN
When you encrypt OX (the first character of PX changed from P to O) you get RY
Encrypting QX (first character of PX changed from P to Q) you get ND
When you encrypt PW (second character of PX changed from X to W) you get KM
Encrypting PY (second character of PX changed from X to Y) you get AL
The basis of the algorithm is:
a) setting up the parameters of a random number generator (RNG) with the secret key. For any given key, the RNG will produce the same sequence of random numbers. i.e. it is repeatable.
b) use the RNG to randomly pick an encoded pair for each possible pair of characters/bytes in a way that has the above property
The algorithm is called Pair Encoding with a Random Number Generator (PERNG pronounced per-ng)
The steps of the algorithm are as follows:
a) setup the parameters of a random number generator (RNG) with the secret key.
b) create a translation matrix as follows:
1) initialize an array of nxn elements where n is the number of characters in the character set (when encrypting bytes n=256). Fill the array with all possible pairs of characters/bytes.
2) sort the array into a random order (this uses the RNG so that the order depends on the secret key)
(The order of this array determines the final translation matrix that is created.)
3) initialize an nxn matrix to empty
4) look at the next element in the array and check if when it is put into the next empty element in the matrix, none of the neighbors will have a matching first or second character/byte.
5) If the element is not suitable, try the next element in the array.
6) If the element is suitable, remove it from the array and save it in the matrix.
7) If no suitable element from the array is found, use the first one in the array anyway.
8) Repeat steps 4 to 7 until the array is empty.
At this point we have a translation matrix that translates a pair of characters/bytes into another pair.
i.e. to find out what the pair XY becomes, lookup matrix[X,Y] to get the new pair: AB (XY and AB are pairs of characters or bytes)
c) try to compress the data (if it does not get smaller leave it uncompressed)
d) optionally add checksum bytes to the end of the data to be encrypted.
e) optionally add a random salt.
f) insert a character at the beginning to indicate what kind of version is allowed to decrypt the data. If the data was encrypted on an expired version set to P else set it to A.
P means only a paid or unexpired version can decrypt it, A means any version can decrypt it.
g) scramble the data with 3 passes using the translation matrix as follows:
-translate the pair made of the characters/bytes: 1st&2nd, the 2nd&3rd, 3rd&4th, ..., last 2
replacing the original pair at each step
-continue scrambling by going in reverse (the end to the beginning)
-scramble again by going forward
h) append an unencrypted header at the start of the encrypted data that indicates:
-the algorithm version# (0=v 1.00, 1=1.01,...)
-type of encryption (symmetric)
-for a file/folder whether the file/folder name is random
-for a file/folder whether it is a file or folder
-a code for compressed/uncompressed
-if there is a checksum
-if there is a salt
i) for a file/folder: append an encrypted version of the path name of the unencrypted file/folder
this is scrambled using the translation matrix like in step g)
j) append the scrambled data from step g).
The resulting characters/bytes are the encrypted version.
To decrypt data:
-create the translation matrix from the secret key
-remove the header
-for a file/folder: remove the path name
-unscramble the remaining data
-if the first character is a P and this is an expired version:
quit with a message to the user that a trial or full version is required to decrypt this
-remove the hash code if any
-verify the checksum if any
-decompress the data if it was compressed.