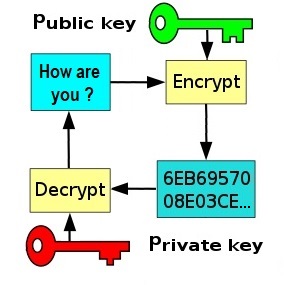
A way to encrypt some data using two different keys.
Encryption is done using a public key.
(This is published so that anyone can send you encrypted data.)
A private key will decrypt the data.
(This is kept private so only you can decrypt data you receive.)
In the diagram, encrypting the message: How are you ? with the public key
produces the encrypted message: 6EB6957008E03CE... .
The private key is used to decrypt: 6EB6957008E03CE...
back to How are you ?
The Data Krypter™ encrypts data using the NTRU-2x2 algorithm.
NTRU-2x2 Asymmetric Encryption Algorithm:
NTRU is one of a family of lattice based encryption methods. (An overview, with an example, is on Wikipedia.)
NTRU-2x2 is based on a variant proposed by Banks and Shparlinksi in 2002. This variant has several important
differences which make it resistant to attack.
A simplified description of the Banks and Shparlinsi algorithm (with some changes) is provided in the steps below.
Public and Private Key Creation:
Setup Random Number Generator:
The creation of a public/private pair of keys is determined by the parameters of a random number generator.
The first step is to randomly choose a creation key of 9-45 characters or use the one supplied by a user.
Setup the parameters of a random number generator (RNG) with the creation key. For any given key, the RNG will produce the same sequence of random numbers. i.e. it is repeatable.
Choose Parameters:
Randomly choose N as a number not divisible by 3 in the range: 821 to 857. (N -1) is the degree of several polynomials to be used below. (The degree is the biggest exponent of the polynomial).
Randomly choose q as a prime number in the range: 4093 to 4283
Set p=3
Create Polynomials:
Select various random polynomials of maximum degree (N -1) in the order explained below.
Each has a modulus value of p, 11 or q from above.
Follow these steps:
-choose z as a random odd number in the range 71 to N/3 (this is the number of non-zero coefficients.)
-choose diff as a random odd number in the range -11 to +11
-set d = (z + diff) / 2
-set d coefficients of the polynomial in the range +1 to +modulus/2
-set (d-diff) coefficients of the polynomial in the range -modulus/2 to -1
note: diff is the (number of positive coefficients) -(number of negative coefficients)
-the remaining coeffients are zero
e.g. if N=821 we might choose z = 105 and diff = +9 so that d = (105 + 9) / 2 = 57 and d - diff = 48
which means we have 105 non-zero coefficients, 57 are positive and 48 are negative
Randomly select a polynomial: G of modulus q that has an inverse G' modulo q
i.e. G * G' (mod q) = 1 where * means multiplying two polynomials then dividing the result by (xN - 1) and keeping the remainder.
Applying (mod q) means each coefficient in the polynomial is divided by q, the remainder is kept, then if it is > q/2 => subtract q so it is converted to the range -q/2 ... -1 since this range = q/2+1,...,q-1 (mod q)
When a polynomial = 1 => all coefficients are zero except the x0 one which = 1
Randomly select a polynomial: f of modulus p that has an inverse f ' modulo p
i.e. f * f ' (mod p) = 1 where * means multiplying two polynomials then dividing the result by (xN - 1) and keeping the remainder.
Applying (mod p) means each coefficient in the polynomial is divided by p, the remainder is kept and if it= 2 it is converted to -1 since p=3 => 2 = -1 mod(p).
When a polynomial = 1 => all coefficients are zero except the x0 one which = 1
Randomly select a polynomial: g of modulus q
Calculate two polynomials from the above ones:
h = G' * g (mod q) and H = G' * f (mod q)
Save key files:
The constants N and q, and the polynomials h and H are stored in a file and used as the public key.
The constants N and q, and the polynomials f ' and G are stored in a file and used as the private key.
(This private key is then encrypted symmetrically using PERNG with the user's master password as the secret key.)
The public and private keys each store 2 polynomials hence the name NTRU-2x2. (pronounced N T R U two by two)
Encryption:
Convert the data to be encrypted into a polynomial m (mod p).
The data is in a character set of 87 possible characters. Every 9 characters can be converted to a number base 3 of <=37 digits. (p=3)
(since 336 < 879 < 337)
Randomly select a polynomial r of modulus 11.
Convert the public key back to the polynomials: h and H.
Calculate the polynomial:
e = p r * h + H * m (mod q)
The polynomial e is converted to a file or characters and becomes the encrypted data.
Decryption:
Convert the private key back to the polynomials: f ' and G.
Convert the encrypted file or characters back to the polynomial e.
Calculate the polynomial:
a = G * e (mod q)
then m = f ' * a (mod p)
m is the original polynomial since:
m = f' * G * [p r * h + H * m (mod q)] (mod p)
= f ' * G * [p r * G' * g (mod q)] + f ' * G * [G' * f * m (mod q)] (mod p)
= f ' * [p r * g] + f ' * [f * m] (mod p) (when a polynomial is multiplied by p then taken (mod p) all coefficients become zero)
= m
Convert the polynomial m back into characters to get the original data.
Hybrid Method:
The above method has a limit on the number of characters of data that can be encrypted.
This is because:
a) the polynomial m, above, has a maximum of N coefficients and N is about 821 => the largest message has 821/37 = 22 groups of 9 characters => a maximum of 198 characters.
b) it is time consuming to multiply polynomials
So a hybrid method is used to encrypt data, as follows:
a) Append an unencrypted header at the start that indicates:
-the algorithm version# (0=v 1.00, 1=1.01,...)
-type of encryption (asymmetric)
-for a file/folder: whether the file/folder name is random
-for a file/folder: whether it is a file or folder
b) Randomly choose a secret key of 9-45 characters.
c) Encrypt the secret key using the public key created above and append to the data.
d) Encrypt the data symmetrically using PERNG with the secret key and append to the data.
For a file/folder: this includes encrypting the path name of the but without any salt or checksum followed by a zero byte.
To decrypt, follow these steps:
a) Split the data into its parts: header, encrypted secret key, path name and encrypted data.
b) Decrypt the secret key using the private key created above.
c) Decrypt the path name, if any, using using PERNG with the secret key.
c) Decrypt the last part using PERNG with the secret key to get the original data.